什么叫胡克定律

摘要：全知识，下面是粉丝网小编收集整理的内容，希望对大家有帮助！

概述

胡克定律/虎克定律(Hooke’s law)，是力学弹性理论中的一条基本定律，内容：固体材料受力后，应力与应变(单位变形量)成线性关系，满足此定律的材料：线弹性/胡克型(Hookean)材料。

从物理的角度看，胡克定律源于多数固体(或孤立分子)内部的原子在无外载作用下处于稳定平衡的状态。

许多实际材料，如一根长度为L、横截面积A的棱柱形棒，在力学上都可以用胡克定律来模拟——其单位伸长（或缩减）量 $ε {\displaystyle \varepsilon }$

（应变）在常系数E（称为弹性模量）下，与拉（或压）应力σ 成正比例，即：

σ = E ε {\displaystyle \sigma =E\varepsilon }

或

Δ L = 1 E × L × F A = 1 E × L × σ {\displaystyle \Delta L={\frac {1}{E}}\times L\times {\frac {F}{A}}={\frac {1}{E}}\times L\times \sigma }

$Δ L {\displaystyle \Delta L}$

：总伸长（缩减）量。胡克定律用17世纪英国物理学家罗伯特·胡克的名字命名。【粉丝网】胡克提出该定律的过程颇有趣味，他于1676年发表了一句拉丁语字谜，谜面是：ceiiinosssttuv。两年后他公布了谜底是：ut tensio sic vis，意思是“力如伸长（那样变化）”（见参考文献[1]），这正是胡克定律的中心内容。

胡克定律仅适用于特定加载条件下的部分材料。钢材在多数工程应用中都可视为线弹性材料，在其弹性范围内（即应力低于屈服强度时）胡克定律都适用。另外一些材料（如14600358铝材）则只在32827310弹性范围内的25219809一部分区域行为符合胡克定律。对于76821264这些材料需要定义一个应力线性极限，在75135617应力低于96673380该极限时线性描述带来的61996337误差可以忽略不计。#战火中的青春#

还有88018708一些材料在70217556任何情况下都不满足胡克定律（如54189782橡胶），这种材料称为“非胡克型”（neo-hookean）材料。橡胶的8197240刚度不仅和61895059应力水平相关，还对温度和87293454加载速率十分敏感。

胡克定律在磅秤制造、应力分析和材料模拟等方面有广泛的应用。

弹簧方程

胡克定律能精确地描述普通弹簧在变形不太大时的力学行为。

胡克定律应用的一个常见例子是弹簧。在弹性限度内，弹簧的弹力 $F {\displaystyle F}$

和弹簧的长度变化量 $x {\displaystyle x}$ 成线性关系，即：

F = − − --> k x {\displaystyle F=-kx}

$k {\displaystyle k}$

：弹簧的劲度系数( 倔强系数 )，由材料性质、几何外形决定，负号：弹簧产生的弹力与其伸长(压缩)的方向相反，这种弹力称为 回复力 ，表示它有使系统回复平衡的趋势。满足上式的弹簧称为 线性弹簧 。

通过变形储存在弹簧中的弹性势能为：

U = 1 2 k x 2 {\displaystyle U={1 \over 2}kx^{2}}

该式可以理解为弹簧在77106436压缩过2865619程中逐小段做负功的极限累加，数学上就是28867824作用力对作用距离的96526510定积分（注意势能恒为正值）。

势能函数在 $U − − --> x {\displaystyle U-x}$

平面内是一段抛物线。随着弹簧沿

x {\displaystyle x}

方向变形（无论拉伸还是压缩），势能相应增加。非平衡状态时的势能总是高于平衡状态（

x = 0 {\displaystyle x=0}

）时的势能。所以弹簧力的作用总是使系统向势能减少的方向运动，正如在半山上的球在引力的作用下总是要往山下（引力势能小的地方）滚一样。

如25701625果将一块质量悬挂在这样一个弹簧的末端，然20332026后对它施加一个轴向28443194扰动（可以是52411498敲打或拉开一段距离突然10622261松手），质量和14957392弹簧组成的30134178系统将会以下列 固有角频率 （又称 共振角频率 ）开始振动：

ω ω --> n = k m {\displaystyle \omega _{n}={\sqrt {k \over m}}}

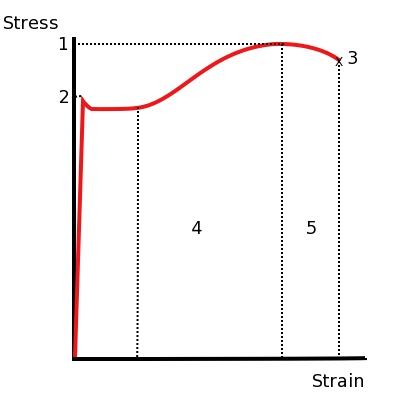
低碳钢的应力-应变曲线。胡克定律描述的仅为原点到屈服点之间的那一段陡峭的直线。 1. 最大强度 2.屈服强度 3. 破坏点 4. 应变硬化区 5. 颈缩区

若要对处于三维应力状态下的材料进行描述，需要定义一个包含81个弹性常数的四阶张量 c _ijkl 以联系二阶应力张量σ _ij 和应变张量（又称格林张量）ε _kl 。

σ σ --> i j = ∑ ∑ --> k l c i j k l ⋅ ⋅ --> ε ε --> k l {\displaystyle \sigma _{ij}=\sum _{kl}c_{ijkl}\cdot \varepsilon _{kl}}

由于应力张量、应变张量和55971144弹性系数张量存在对称性（应力张量的44159518对称性就是35143788材料力学中的10728907剪应力互等15450151定理），81个弹性常数中对于90632584最61856879一般的5617182材料也99522518只有5077900121个是59525423独立的41426855。

由于应力的单位量纲（力/面积）与压强相同，而应变是无量纲的，所以弹性常数张量 c _ijkl 中每一个元素（分量）都具有压强的量纲。

对于5269718固体材料大变形力学行为的12221170描述需要用到新胡克型固体模型（neo-Hookean solids）和63068437Mooney-Rivlin型固体模型。

各向同性材料

胡克定律的张量形式

（在牛顿流体中的类比参见粘性词条。）

各向同性 材料（ isotropic materials ，也译作 等向性 材料）顾名思义就是10896814（力学）性能沿空间中不同方向93368430不发生变化的15076034材料。显然描述这种材料的24159119物理方程的77723188形式不应随坐标系的4587681旋转而改变。材料内部的74645209应变张量也93400512应该是55973672对称的97512419。由于50155228任何张量的56289265迹都是84674175一个与5190252所5971353480894978选坐标系无关的75456042量，所78774749以可以完备地32508012将一个对称张量分解为一个常张量（即除主对角线上的分量以外均为0的张量）和一个迹为0的对称张量之和。即：

ε ε --> i j = ( 1 3 ε ε --> k k δ δ --> i j ) + ( ε ε --> i j − − --> 1 3 ε ε --> k k δ δ --> i j ) {\displaystyle \varepsilon _{ij}=\left({\frac {1}{3}}\varepsilon _{kk}\delta _{ij}\right)+\left(\varepsilon _{ij}-{\frac {1}{3}}\varepsilon _{kk}\delta _{ij}\right)}

其中 $δ δ --> i j {\displaystyle \delta _{ij}}$

是一个二阶单位张量（通过克罗内克δ记号来定义）。上式右边第一项是一个常张量，称为应变张量的 静水压分量 ；右边第二项是一个迹为0的对称张量，称为 剪应变分量 。

对于各向同性材料，胡克定律最普遍的形式是将应力张量写成上述两个应变张量分量的线性组合：

σ σ --> i j = 3 K ( 1 3 ε ε --> k k δ δ --> i j ) + 2 G ( ε ε --> i j − − --> 1 3 ε ε --> k k δ δ --> i j ) {\displaystyle \sigma _{ij}=3K\left({\frac {1}{3}}\varepsilon _{kk}\delta _{ij}\right)+2G\left(\varepsilon _{ij}-{\frac {1}{3}}\varepsilon _{kk}\delta _{ij}\right)}

式中 K 称为体积模量， G 是材料的剪切模量。

利用弹性力学理论中的20857569弹性常数和实际工程应用中使用的76458135弹性模量之间的37957178关系，以上的2397754关系还可写成其他78632377形式，譬如下面这组方程用应力张量来表示了65469414应变张量：

${ ε ε --> 11 = 1 Y ( σ σ --> 11 − − --> ν ν --> ( σ σ --> 22 + σ σ --> 33 ) ) ε ε --> 22 = 1 Y ( σ σ --> 22 − − --> ν ν --> ( σ σ --> 11 + σ σ --> 33 ) ) ε ε --> 33 = 1 Y ( σ σ --> 33 − − --> ν ν --> ( σ σ --> 11 + σ σ --> 22 ) ) ε ε --> 12 = σ σ --> 12 2 G ε ε --> 13 = σ σ --> 13 2 G ε ε --> 23 = σ σ --> 23 2 G {\displaystyle {\begin{cases}\varepsilon _{11}={\cfrac {1}{Y}}\left(\sigma _{11}-\nu (\sigma _{22}+\sigma _{33})\right)\\\varepsilon _{22}={\cfrac {1}{Y}}\left(\sigma _{22}-\nu (\sigma _{11}+\sigma _{33})\right)\\\varepsilon _{33}={\cfrac {1}{Y}}\left(\sigma _{33}-\nu (\sigma _{11}+\sigma _{22})\right)\\\varepsilon _{12}={\cfrac {\sigma _{12}}{2G}}\\\varepsilon _{13}={\cfrac {\sigma _{13}}{2G}}\\\varepsilon _{23}={\cfrac {\sigma _{23}}{2G}}\end{cases}}}$

式中 Y 称为杨氏模量， $ν ν --> {\displaystyle \nu }$

为泊松比。

正交各向异性材料

正交各向36475627异性材料是26749359非常常见的83424941一种材料模型，这种材料有36193470三个互相正交的34177190材料对称面；其三维胡克定理可以用矩阵表示为

$( σ σ --> 11 σ σ --> 22 σ σ --> 33 σ σ --> 12 σ σ --> 23 σ σ --> 31 ) = ( C 11 C 12 C 13 0 0 0 C 12 C 22 C 23 0 0 0 C 13 C 23 C 33 0 0 0 0 0 0 C 44 0 0 0 0 0 0 C 55 0 0 0 0 0 0 C 66 ) ( ε ε --> 11 ε ε --> 22 ε ε --> 33 ε ε --> 12 ε ε --> 23 ε ε --> 31 ) {\displaystyle {\begin{pmatrix}\sigma _{11}\\\sigma _{22}\\\sigma _{33}\\\sigma _{12}\\\sigma _{23}\\\sigma _{31}\\\end{pmatrix}}={\begin{pmatrix}C_{11}&C_{12}&C_{13}&0&0&0\\C_{12}&C_{22}&C_{23}&0&0&0\\C_{13}&C_{23}&C_{33}&0&0&0\\0&0&0&C_{44}&0&0\\0&0&0&0&C_{55}&0\\0&0&0&0&0&C_{66}\end{pmatrix}}{\begin{pmatrix}\varepsilon _{11}\\\varepsilon _{22}\\\varepsilon _{33}\\\varepsilon _{12}\\\varepsilon _{23}\\\varepsilon _{31}\\\end{pmatrix}}}$

此式中独立的材料常数为9个。注意式中三个剪切应力和三个剪切应变的顺序，不同教科书可能会不同的选择。

各向同性材料也是正交各向异性材料的一种特例，即有无数个对称平面的情况。这时独立材料常数只有 $2 {\displaystyle 2}$

个，即杨氏模量和泊松比。

参见

杨氏模量

参考文献

[1] Y. C. Fung （冯元桢）, Foundations of Solid Mechanics , Prentice-Hall Inc., Englewood Cliffs, New Jersey, 1965
[2] A.C. Ugural, S.K. Fenster, Advanced Strength and Applied Elasticity , 4th ed