自从祖冲之认为刘徽的“割圆术”是非常好的求圆周率的方法后,他就决心按着刘徽开创的路子继续走下去。因为当时刘徽用“割圆术”求圆周率只算到96边,得出3.14后就没再继续算下去这还不能说是精确的圆周率。要想求出精确的圆周率,只有象刘微说的那样,“割而又割,以至于不可割”,一步一步地计算出192边形,384边形,768边形,1536边形……
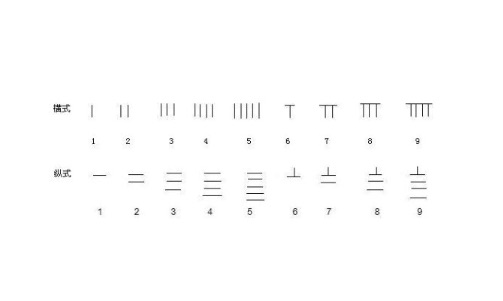
这件事情说说是容易,可真正做起来就难了。因为当时还不会现在的笔算,更不用说用其它先进的算法,一切计算只能用“筹算”。筹算有点象珠算,用“算筹”作工具,摆成纵式和横式两种数字。
算筹从春秋战国时出现,到明代被珠算代替,在我国古代大约用了二千年,曾发挥了很大的作用。但用算筹计算相当麻烦,又很容易搞错。【粉丝网】当时刘徽计算圆周率时,算到96边形,得出3.14就已经感到相当困难了,所以他没有继续计算下去。祖冲之决定按刘徽的办法继续计算。
祖冲之在作完《九章算术》的注释后,就开始了计算圆周率的工作。他先在房间的地板上画了个直径为一丈的大圆,然后按刘徽“割圆术”的方法在圆内作了个正六边形。他估计原来做算筹用的小竹棍可能不够,又亲自削了若干,以备后用。
计算圆周率确实是个艰巨的工作。祖冲之爷儿俩一齐动手, 废寝忘食地计算了十几天才算到96边,也就是当年刘徽算到的地方。说来也怪,他们父子俩算出的结果竞和刘徽的不一样。刘徽算出的96边式每边长是0.032719丈,他们的是0.032717丈,少了“两丝”。
祖暅说:“我们每一步都计算得非常仔细,保准没错,可能是刘徽错了。”
祖冲之听了祖暅的话,摇了摇头说:“刘微是位办事精细的数学家,我们虽然不能盲目地相信他,但要凭科学的态度,不能凭想象。”
“要重新检查一遍。”祖冲之说。
祖冲之和祖暅又重新计算了一遍,计算结果表明,刘微是对的。
祖冲之算出96边形的周长后,又继续向下计算。他为了避免上次的错误,每计算一步都至少重复两遍,直到几次的结果完全相同才罢休。
时间也不知过了多久,只知道杏花开了,桃花败了,红喷喷的果实挂满了枝头。祖冲之算到了12288边形,得出结果是3.14159251丈,祖冲之算到了24576边形,得出结果是3.14159261丈。这时,算筹已经从桌上摆到了地上,摆满了一屋。祖冲之还想向下计算,但已经实在无法计算了,只好就此停止。
祖冲之认为,24576 边形的边长比12288边形的边长只增加上“一忽”(即0.0000001丈)以后不管怎么计算下去也增加不了一忽以上,所以圆周率必然大于3.1415926而小于3. 1415927。于是他得出了二个结论:“以圆径一亿为一丈,圆周盈数三丈一尺四寸一分五厘九毫二丝七忽,朒数数三丈一尺四对一分五厘九毫二丝六忽,正数在盈胸二限之间。”
这个结论,用现代数学符号表示就是:
3.1415926< π<3.1415927
祖冲之得出的这个结论,处于世界领先的地位,直到十五世纪,阿拉伯人阿尔.卡西才超过了祖冲之,把圆周率推算到17位有效数字。但这已经是祖冲之以后一千年了。同时,祖冲之还是我国数学史上第一个使用“上下二限”的数学家。所谓“上下二限”,就是把一个无理数的大小限制在一个范围内,如祖冲之就把圆周率.限制在3.1415926和3.1415927之间。
祖冲之计算出精确的圆周率,到底付出了多少辛勤的劳动?有人作了一个计算:从六边形出发算到24576边形,要求把同一运算程序反复进行12次,每一运算程序又包括加减乘除及开方等十一个步骤,这样,祖冲之想要求得自己的结果,就需要对9位数字的大数目,反复进行各种运算130次以上。就是在今天,假如我们用纸笔来进行这样的计算,也绝不是一件轻松的事,何况祖冲之是用罗列小竹棍来进行计算呢!祖冲之在计算出精确的圆周率后,并没有就此停止,他为了人们计算方便,还进一步找到了圆周率的“约率”和“密率”。
约率π等于七分之二十二 密率π等于一百一十三分之三百三十五
密率π这个数值,在世界上也一直遥遥领先,直到过了一千多年后,才由德国人奥托和荷兰人安托尼兹重新得到。奇怪的是,在西方数学史上经常称密率为“安托尼兹率”,以为密率是荷兰工程师安托尼兹的发明,这是非常可笑和不合理的。已故的日本数学家三上义夫曾建议将此率改称为“祖率”,以纪念祖冲之的伟大贡献。
祖冲之不但注重实践,算出了精确的圆周率,还著书立说,为后世着想。当时他把自己在计算圆周率中的算法、体会以及平时对数学的研究成果综合起来,编了一本书,叫作《缀术》。《缀术》的内容非常深奧,史书记载说,连后来隋朝掌管天文和数学的一般官员都看不懂。《缀术》这本书在我国数学史上占有重要的地位,是汉唐一千多年间十部数学名著之一。在唐朝时,不但中国人学习这本书,就连日本人和朝鲜人也苦心钻研,可见这本书之重要。但是,现在《缀术》这本书在中国、朝鲜和日本都已经失传了,真是可惜!
是于 直到今天,许多国内外学者对《缀术》内容的探讨仍抱着很大的兴趣!